Chapter-1 (Complexity Analysis)

        Content

• Introduction of Data Structure
• Classification of Data Structure
• Asymptotic Notation

                                                  Definition

A data structure can be described as a set of domains d, a set of functions F and a set of rules A.

              D = {d, F, A},

where, D refers to Data structure d refers to Domain variable,

F refers to a set of functions or procedures operating on domain variables,

A is a set of rules governing the operations of these functions on the domain variable.

OR,

In computer science, a data structure is a data organization, management and storage format that enables access and modification.

In simple words, Data Structure is a way of storing data in computer.

                                                                                  Importance

• The study of data structure helps programmers to store and manipulate data efficiently.
• They also provide various methods to organize and represent the data within the computer’s memory
• Data structure is very important since it governs the types of operations we perform on the data, and the competency of the operations carried out
• It also governs how dynamic we can be in dealing with our data.

                                                        Classification of Data Structures

• Primitive
• Non-primitive

These can be be further classified:-

Primitive Data Structure:

• Primitive data structures are those which are predefined way of storing data by the system. And the set of operations that can be performed on these data are also predefined.
  
  
• Primitive Data Structures are directly operated upon by machine-level instructions. 
• Primitive data structures are char, int, float, double. 

Non-Primitive Data Structure:

• Non primitive data structure are more sophisticated data structures. 

• Non primitive data structure are derived from the primitive data structures.

• The non-primitive data structures emphasize on structuring of a group of homogeneous (same type) or heterogeneous (different type)data items.

Further divided into linear and non-linear data structure:

        Linear Data Structure:

• A data structure that maintains a linear relationship among its elements is called a linear data structure.
• Here, the data is arranged in a linear But in the memory, the arrangement may not be sequential.Non Linear Data Structure:
• Non-linear data structure is a kind of data structure in which data elements are not arranged in a sequential order
• There is a hierarchical relationship between individual data items.
• Here, the insertion and deletion of data is not possible in a linear fashion.

                                                      Abstract Data Type (ADT)

• Abstract Data type (ADT) is a type (or class) for objects whose behavior is defined by a set of value and a set of operations.
• The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented.
• This means that we are concerned only with what the data is representing and not with how it will eventually be constructed.
• Abstract Data Type(ADT) is a data type, where only behavior is defined but not implemented.
• Abstract Data type is a theoretical concept.
• An abstract data type (ADT) is a mathematical model for data types where a data type is defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations.
• A set of data values and associated operations that are precisely specified independent of any implementation.
• For Example : Stack is an Abstract Data Type. A stack ADT can have the operations push, pop, These three operations define what the type can be irrespective of the language of the implementation.
• So we can say, Primitive data types are a form of Abstract data type. It is just that they are provided by the language makers and are very specific to the language. So basically there are 2 types of data types primitives and user defined. But both are abstract data types.

                                                                      Algorithm

• An algorithm is a precise specification of a sequence of instructions to be carried out in order to solve a given problem.
• Each instruction tells what task is to be done.
• There should be a finite number of instructions in an algorithm and each instruction should be executed in a finite amount of time.

Properties of Algorithms

• Input: A number of quantities are provided to an algorithm initially before the algorithm These quantities are inputs which are processed by the
• Effectiveness: Each step must be carried out in finite time.
• Finiteness: Algorithms must terminate after finite time or step
• Output: An algorithm must have output.
• Definiteness: Each step must be clear and unambiguous.
• Correctness: Correct set of output values must be produced from the each set of inputs.
  

Example:

Write an algorithm to find the greatest number among three numbers:

Step 1: Read three numbers and store them in X, Y and Z

Step 2: Compare X and Y. if X is greater than Y then go to step 5 else step 3

Step 3: Compare Y and Z. if Y is greater than Z then print “Y is greatest” and go to step 7 otherwise go to step 4

Step 4: Print “Z is greatest” and go to step 7

Step 5: Compare X and Z. if X is greater than Z then print “X is greatest” and go to step 7 otherwise go to step 6

Step 6: Print “Z is greatest” and go to step 7

Step 7: Stop

Types of algorithms

• Simple Recursive algorithms
• Dynamic programming algorithm
• Backtracking algorithm
• Divide and conquer algorithm
• greedy algorithm
• Brute Force algorithm
• Randomized algorithm

How to choose algorithm among available?

We need to learn how to compare the performance of different algorithms and choose the best one to solve a particular problem.

While analyzing an algorithm, we mostly consider time complexity and space complexity.

Time Complexity

Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Time complexity of an algorithm is defined as the total time required by an algorithm to complete a certain task It is mostly measured in number of steps required to compare the task rather than the exact time required by the algorithm Time Complexity of algorithm/code is not equal to the actual time required to execute a particular code but the number of times a statement executes.

Space Complexity

It the amount of memory space required by the algorithm, during its execution. Space complexity must be taken seriously for the multi-user systems and in situations where limited memory is available.

Asymptotic Notation

• When it comes to analyzing the complexity of any algorithm in terms of time and space, we can never provide an exact number to define time and space required by the algorithm, instead we express it using some standard notations, also known as Asymptotic Notations.
• Asymptotic notation are the language that allows us to analyze an algorithm’s running time by identifying its behavior as the input size for the algorithm increases. This is known as algorithm growth rate.
• Asymptotic notations are the mathematical notations used to describe the running time of an algorithm when the input tends towards a particular value or a limiting value.
• Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it works in a constant time.

Types of asymptotic notation

We use three types of asymptotic notations to represent the growth of any algorithm, as input increases:

• Big Theta (Θ)
• Big Oh(O)
• Big Omega (Ω)

Big-O Notation (O-notation)

Big-oh notation is used to express the asymptotic behavior of the function. It tells how fast the function grows or declines and measures the maximum amount of time required to complete the program execution. It is the representation of the worst case time complexity or the longest amount of time an algorithm can possibly take to complete.

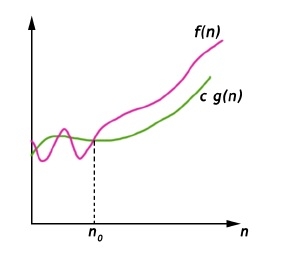
Big-Omega Notation (Ω-notation)

Big-Omega (Ω) notation gives a lower bound for a function f(n) to within a constant factor.

We write f(n) = Ω(g(n)), If there are positive constants n0 and c such that, to the right of n₀ the f(n) always lies on or above c*g(n).

Ω(g(n)) = { f(n) : There exist positive constant c and n0 such that 0 ≤ c g(n) ≤ f(n), for all n ≤ n₀}

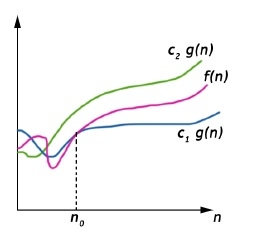
Big-Theta Notation (Θ-notation)

Theta notation encloses the function from above and below. Since it represents the upper and the lower bound of the running time of an algorithm, it is used for analyzing the average case complexity of an algorithm.

Big-Theta(Θ) notation gives bound for a function f(n) to within a constant factor.

We write f(n) = Θ(g(n)), If there are positive constants n0 and c₁ and c₂ such that, to the right of n₀ the f(n) always lies between c₁*g(n) and c₂*g(n) inclusive.

Θ(g(n)) = {f(n) : There exist positive constant c₁, c₂ and n₀ such that 0 ≤ c₁ g(n) ≤ f(n) ≤ c₂ g(n), for all n ≥ n₀}

Amortized Complexity

• Classical asymptotic analysis gives worst case analysis of each operation without taking the effect of one operation on the other
• Before, we analyze the performance of algorithm based on best case, worst case, and average case.

• We see for a given input whether an algorithm comes under best case worst case or average case.
  
• If an algorithm comes under best case what will be its running time.
• If an algorithm comes under worst case what will be its running time.
• If an algorithm comes under average case what will be its running time.
• Normally when we analyze complexity of algorithm, the sequence of one input given to that algorithm doesnot effect the running time  of other input sequence.
• But what if the one input sequence does effect the running time of other input sequence.
• In such case our classical analysis theory won’t work, there we should go for amortized analysis or complexity.
• If there is a sequence of input and same input affect the running time of other input, then we should go for amortized complexity.

Amortized Analysis

• Amortized analysis is the analysis for a series of operations, an interplay between operations, and thus yielding an analysis which is precise and depicts a micro-level analysis.
• Amortized analysis is used for algorithm where an occasional operation is slow but most of the other operation are fast.

• In amortized analysis we analyze a sequence of operation and guarantee a worst-case average time which is lower than the worst-case time of particular expensive operation.
• Amortized analysis can be used to show that the average cost of an operation is small, if one averages over a sequence of operations, even though a single operation might be expensive.
• Amortized analysis differs from average-case analysis in that probability is not involved; an amortized analysis guarantees the average performance of each operation in the worst case.

Deterministic and Non-Deterministic Algorithm

• Deterministic algorithm is the algorithm which, given a particular input will always produce the same output, with the underlying machine always passing through the same sequence of states.
• In other words, Deterministic algorithm will always come up with the same result given the same inputs.

• Deterministic algorithms can be defined in terms of a state machine: a state describes what a machine is doing at a particular instant in time.
• State machines pass in a discrete manner from one state to another. Just after we enter the input, the machine is in its initial state or start If the machine is deterministic, this means that from this point onwards, its current state determines what its next state will be; its course through the set of states is predetermined.
• Note that a machine can be deterministic and still never stop or finish, and therefore fail to deliver a result.

What You Need To Know About Deterministic Algorithm

1. Deterministic algorithm is the algorithm which, given a particular input will always produce the same output, with the underlying machine always passing through the same sequence of states.
2. In deterministic algorithm the path of execution for algorithm is same in every execution.
3. On the basis of execution and outcome in case of Deterministic algorithm, they are also classified as reliable algorithms as for a particular input instructions the machine will give always the same output.
4. In Deterministic Algorithms execution, the target machine executes the same instruction and results same outcome which is not dependent on the way or process in which instruction get executed.
5. As outcome is known and is consistent on different executions so deterministic algorithm takes polynomial time for their execution.

1. A nondeterministic algorithm is an algorithm that, even for same input, can exhibit different behaviors on different In other words, it is an algorithm in which the result of every algorithm is not uniquely defined and result could be random.
2. An algorithm that solves a problem in nondeterministic polynomial time can run in polynomial time or exponential time depending on the choices it makes during. The nondeterministic algorithms are often used to find an approximation to a solution, when the exact solution would be too costly using a deterministic one.
3. A nondeterministic algorithm is different from its more familiar deterministic counterpart in its ability to arrive at outcomes using various routes. If a deterministic algorithm represents a single path from an input to an outcome, a nondeterministic algorithm represents a single path stemming into many paths, some of which may arrive at the same output and some of which may arrive at unique outputs.

  What Makes An Algorithm Non- deterministic?

1. If it uses external state other than the input, such as user input, a global variable, a hardware timer value, a random value, or stored disk data.
2. If it operates in a way that is timing-sensitive, for example if it has multiple processors writing to the same data at the same In this case, the precise order in which each processor writes its data will affect the result.
3. If a hardware error causes its state to change in an unexpected way.

Class P:

• A problem belongs to the class of P problems if it can be solved in polynomial time with a deterministic algorithm

Class NP:

• A problem belongs to the class of NP problems if it can be solved in polynomial time with a nondeterministic algorithms.
  

• P problems are obviously NP problems are also tractable, but only when nondeterministic algorithms are used.